第二十二章 各种积分间的联系和场论初步

§1 各种积分间的联系

一 Green公式

定义1 一个平面区域，如果全落在此区域内的任一条封闭曲线都可以不经过以外的点而连续地收缩为一点，则称此区域为单连通的，否则称为复连通的。

定理1 设是以光滑曲线为边界的平面单连通区域，设函数，在及上连续并具有关于自变量和的连续偏导数，则有：

这里右端积分路径的方向是和区域正相联系的，既当一人沿着曲线行走时区域恒在他的左边。

注：Green公式同时揭示了平面上某区域内的二维积分与该边界上的一个特定的第二类曲线积分之间的关系；

注：常用于第二类曲线积分，有时用来计算二重积分在Green公式中。

例：求第二类曲线积分I= ,是上半圆周： 方向从。

例：设函数，有其二阶连续偏导数，记，证明

(i)；

(ii)  ；(3)。

例：（用Green公式求曲面的面积）求曲线所围图形的面积。

注：在使用Green公式时，应注意“助线法”的使用。

二  Gauss公式

定理2 设空间二维单连通有界闭区域的边界曲面是光滑的，又设函数，，在及上具有关于的连续偏导数，则有：

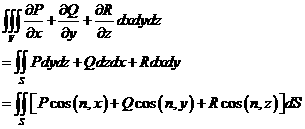
这里为曲面的外法线方向，第二个积分沿曲面的外侧。

注：①Gauss公式揭示了中的某区域内的三重积分和这一区域的边界上的特定曲面积分之间的关系；②与 Green公式一样，由Gauss公式可计算某些空间立体积分：

。

例：求积分 I=，: 沿外侧。

例：求积分 其中是锥面。

注：在使用Gauss公式时，应注意“助面法”的使用。

三  Stokes公式

定理3（Stokes）设光滑曲面的边界为光滑曲线，设函数，，在曲面及曲线上具有关于的连续偏导数，则有：

曲线积分的方向和曲面的侧按右手法则联系。

注：右端积分是一个第二类曲面积分，左端的积分是一个第二类曲线积分。所以Stokes公式是第二类曲面积分和第二类曲线积分的一个纽带。

例：求曲线积分，其中是柱面x和平面的交线,其方向从轴正向望去，已知方向是逆时针。

§2 曲线积分和路径的无关性

l 引言

第二类曲线积分不仅与曲线的起点和终点有关，而且也与所沿的积分路径有关。对同一个起点和同一个重点，沿不同的路径所得到的第二类曲线积分一般是不相同的。在什么样的条件下第二类曲线积分与积分路径无关而仅与曲线的起点和重点有关呢？下面我们在平面中情形来讨论这个问题。

定理1 若函数，在区域上有连续的偏导数，是单连通区域，则下列命题等价：

⑴ 对D内任意一条闭曲线，有

。

⑵ 对 内任意一条闭曲线，曲线积分

与路径无关（只依赖曲线的端点）。

⑶存在可微函数，使得内成立；

⑷在D内处处成立。

定义1 当曲线积分和路径无关时，即满足上面的诸条件时，如令点固定而点为区域内任意一点，那么

在内连续并且单值。这个函数称为的原函数。

原函数的求法：

（1）；

或

（2）。

例：求原函数

（1）;

（2）。

定义2 只绕奇点一周的闭路上的积分值叫做区域的循环常数，记为。于是，对内任一闭路

，

这里为沿逆时针方向绕的圈数。

例：证明关于奇点的循环常数是，从而积分与路径无关。

§3 场论初步

一 场的概念

物理量在空间或一部分空间上的分布就称为场。场分为不定常场和定常场。

二 向量场的散度和旋度

设有一向量场，为一闭曲面所包围的空间区域，为曲面上向外法线，由高斯公式得

。

定义1 量称为向量的散度，它形成一个数量场，记为

。

利用散度的定义，高斯公式可写为

，

这是高斯公式向量形式。它说明：向量通过闭曲面的流量等于这个向量的散度在所包围的区域上的三重积分。

定义2  称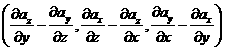向量为向量的旋度，记为：

。

利用的定义，Stokes公式可改写为向量形式如下：

。

它说明：向量沿闭曲线的环流量等于它的旋度通过以为边界所张的任意曲面的流量。

散度和旋度的定义。

例：求在点的散度和旋度。

例：证明。