2009/2010山东理工大学《高等数学》A卷
一、 填空题(每小题2分共20分)
1. 函数![]() 的定义域是
的定义域是
2. 极限 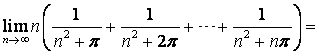
3. 极限 ![]()
4. 函数![]() 的微分
的微分![]()
5. 曲线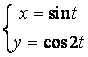 在
在![]() 处的切线方程为
处的切线方程为
6. 已知函数![]() 则
则![]()
7. 已知![]() 则
则![]()
8. 若函数![]() 连续,则极限
连续,则极限
9. 抛物线![]() 与直线
与直线![]() 及
及![]() 轴所围成的图形绕
轴所围成的图形绕![]() 轴旋转一周所得的旋转体的体积为
轴旋转一周所得的旋转体的体积为
10. 已知水深![]() 处的压强为
处的压强为![]() 微(其中
微(其中![]() 是水中的密度,g是重力加速度),若宽为a高为b的矩形闸门铅直放入水中,上沿与水面平齐,则闸门一侧所受的水压力为
是水中的密度,g是重力加速度),若宽为a高为b的矩形闸门铅直放入水中,上沿与水面平齐,则闸门一侧所受的水压力为
二、单项选择题(每小题2分共10分)
1. 数列![]() 有界是数列
有界是数列![]() 下收敛的( )
下收敛的( )
A 充分条件. B 必要条件. C 充分必要条件. D 既非充分又非必要条件.
2. 设 ( )
( )
A ![]() . B
. B
![]() . C
. C ![]() . D
. D ![]() .
.
3. 当![]() 时,
时,![]() 与
与![]() 相比(
)
相比(
)
A 是同阶但非等价无穷小. B是等价无穷小. C是低阶无穷小. D 无法比较
4. 设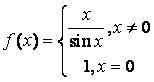 则
则![]() 处是此函数的( )
处是此函数的( )
A 可去间断点. B无穷间断点. C 振荡间断点. D连续点.
5. 设函数 则
则![]() 在
在![]() 处的(
)
处的(
)
A 左右导数存在. B左导数存在,右导数不存在.
C 左导数不存在,右导数存在. D 左、右导数都不存在.
三、求解下列各题(每小题5分共30分)
1. 计算极限 ![]() .
2. 设
.
2. 设
![]() 求
求![]()
3. 计算不定积分 4. 计算定积分
4. 计算定积分![]()
5. 计算定积分![]() 已知函数
已知函数
![]() ,计算
,计算![]()
四、(8分)
设![]() ,证明不等式
,证明不等式 ![]()
五、(10分)
求曲线![]() 的拐点、凹凸区间及单调区间
的拐点、凹凸区间及单调区间
六、(8分)
求微分方程![]() 的通解.
的通解.
七、(8分)
计算反常积分 (其中
(其中![]() ),并计算使得
),并计算使得![]() 最小的k值
最小的k值
八、(6分)
对于每个正整数![]() , 证明方程
, 证明方程![]() 在
在![]() 内必有唯一的实根
内必有唯一的实根![]() ,且由根
,且由根![]() 组成的数列
组成的数列![]() 收敛,并求极限
收敛,并求极限![]()