高等数学上学期模拟试题（一）
一、选择题：（12分）
1．设f (x)在x0处可导，g (x)在x0处不可导，那么在x0处 .
（A）f (x)+ g (x) 与 f (x)·g (x)在x0处都不可导；
（B）f (x)+ g (x) 与 f (x)·g (x)在x0处都可导；
（C）f (x)+ g (x) 未必不可导，而 f (x)·g (x)一定不可导；
（D）f (x)+ g (x) 一定不可导，而 f (x)·g (x)未必不可导；
2．设 
，则 
的值等于 .
（A）0； （B）－2－27； （C）2－272－27； （D）227
3．设f (x) 在[a, b]上连续，积分中值定理： 
中的 
是 .
（A）[a, b]上任一点；
（B）在[a, b]上至少存在某一点；
（C）[a, b]上唯一的某一点； （D）[a, b]上的中点
4．设函数y = f (x)可导，且 
，则当 
时，该函数在x0处的微分是
.
（A）Δx的等阶无穷小；
（B）Δx的同阶无穷小；
（C）Δx的高阶无穷小；
（D）Δx的低阶无穷小
二、填空题：（14分）
1． 
= .
2．函数 
在[-1，1]上不能有罗尔定理的结论，其原因是由于f (x)不满足罗尔定理 的条件。
3．设 
，则 
4．设 
，则 
=
.
5．由曲线 
和直线 
所围成的图形绕直线y=－1旋转一周所得旋转体的体积可用定积分表示为
.
三、计算题（4×3=52分）
1．求极限 
2． 
3．求曲线 
与x轴所围图形绕x轴旋转一周的旋转体之体积。
4．求极限 
. 5． 
，求 
.
6．求 
在x=1处的切线方程.
7．设 
，求 
8．设 
，且 
存在，求f (2).
9．已知 
，求 
.
10．求 
.
四、若曲线y = f (x)上点(x, y)处的切线斜率与x3成正比例，并知道曲线通过点A (1,6)和B (2,-9)，求该曲线的方程。（4分）
五、设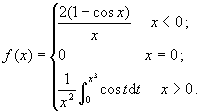 
讨论f (x)在x = 0处的连续性和可导性。（5分）
六、设f (x)在[0,1]上连续，且0< f (x)<1，求证方程 
在（0,1）内有且只有一个实根。（4分）
七、求通过点（0,0）点（1,2）的抛物线，它满足如下条件：
①对称轴平行于y轴，且图形是凸的。
②它与x轴所围成的面积最小。（5分）
八、设函数f (x)在[a,b]上具有连续的二阶导数，且 
.证明 
（4分）