高等数学上学期模拟试题（二）

一、填空

1．极限 = .

2．设 ，则y′= .

3．积分 和 的大小关系是 .

4． .

5．设k是实常数，函数f (x)= 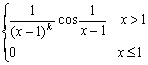.若 存在，则k的取值范围是 .

二、选择：

1．设 ，则 等于： .

（A）g (x²)； （B）2xg (x) （C）x²g(x²)； （D）2xg (x²)

2．设f (x) 在x = x₀处附近四阶连续可导且 ， ，则有：

（A）y = f (x)在x = x₀有极大值； （B）y = f (x)在x = x₀有极小值；

（C）y = f (x)在x = x₀有拐点； （D）y = f (x)在x = x₀无极值也无拐点。

3．对于不定积分 ，在下列等式中正确的是 .

（A） ； （B） ；

（C） ； （D） .

4．已知f (x) 在x = 0的某邻域内连续，且f (0) =0， ，则在x=0处，f (x) .

（A）不可导 （B）可导且 （C）取得极大值 （D）取得极小值

三、1.若f (x)有n阶导数，试用数学归纳法证明：

2．求曲线 的拐点坐标。

3．作 的图形。

4．求曲线 上曲率最大的点的坐标。

四、一曲线过原点，且在任一点（x,y）的切线的斜率等于2x，求该曲线方程。

五、当a为何值时，抛物线y=x²与三直线x = a，x = a+1，y= 0所围成的图形面积最小？

六、设曲线方程为 ，求此曲线在横坐标x=1处的法线方程。

七、直线y = ax+b经过点(2,1)，且使积分 的值最小，求a、b之值。

八、求

九、求

十、设f (x) 具有二阶导数，在x = 0的某去心邻域内f (x) ≠0，且 ，求 .

十一、设f (x)在[0,1]上连续，证明 。

十二、设 在 有意义，试证明：