高等数学上学期模拟试题(三)
一、填空题(每小题3分,共9分,填错或不填均得零分)
1.设 ![]() ,则
,则 ![]() =
.
=
.
2. ![]() .
.
3.设 ![]() ,且f [g (x)]=lnx,则
,且f [g (x)]=lnx,则 ![]() =
.
=
.
二、选择题(每小题3分,共9分,选错或不选均不得零分)
1.设f (x)在[0,1]上有 ![]() >0,且
>0,且 ![]() =0,则
=0,则 ![]() (1),
(1), ![]() (0),f (1)-f (0),或f (0)-f (1)的大小顺序是:( )
(0),f (1)-f (0),或f (0)-f (1)的大小顺序是:( )
(A) ![]() (1)>
(1)> ![]() (0)>
f (1)-f (0); (B)
(0)>
f (1)-f (0); (B) ![]() (1) > f (1) -f (0)>
(1) > f (1) -f (0)> ![]() (0);
(0);
(C)f (1)-f (0)> ![]() (1)>
(1)>
![]() (0); (D)
(0); (D) ![]() (1) > f (0) -f (1)>
(1) > f (0) -f (1)> ![]() (0)
(0)
2.设ab<0, ![]() 则在a<x<b内使f (b) -f (a) = f(ξ)(b-a)成立的点ξ:( )
则在a<x<b内使f (b) -f (a) = f(ξ)(b-a)成立的点ξ:( )
(A)只有一点; (B)有两个点; (C)不存在; (D)是否存在与a,b之值有关.
3. 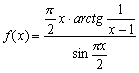 的间断点类型是( )
的间断点类型是( )
(A)可去;
(B)跳跃; (C)无穷; (D)A、B、C都有.
三、解答下列各题(每题6分,共54分)
1.设 ![]() 为常数,(a≠1),求
为常数,(a≠1),求 ![]()
2.求 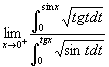
3.设 ![]() ,求
,求 ![]()
4. 设 ![]() ,且
,且 ![]() ,求
,求 ![]()
5. ![]()
6. 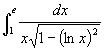
7.设 ![]() ,
, ![]() ,…,
,…, ![]() ,…,证明
,…,证明 ![]() 存在,并求出它。
存在,并求出它。
8.已知 ![]() ,求
,求 ![]() 的值。
的值。
9. 计算积分  (n=正奇数)
(n=正奇数)
四、(本题8分),设函数 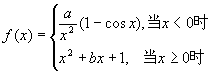 ,在(
,在( ![]() ,
, ![]() )上处处连续,可导,求a,b的值。
)上处处连续,可导,求a,b的值。
五、(本题8分)在椭圆 ![]() 内作底边平行于x轴的内接三角形,求最大三角形的面积。
内作底边平行于x轴的内接三角形,求最大三角形的面积。
六、(本题6分)求曲线 ![]() ,直线
,直线 ![]() 及
及 ![]() 轴三者围成的图形绕
轴三者围成的图形绕 ![]() 轴旋转所成旋转体的体积。
轴旋转所成旋转体的体积。
七、(本题6分)设函数 ![]() 在闭区间[0,1]上可微,且满足
在闭区间[0,1]上可微,且满足 ![]() ,求证在(0,1)内至少存一点
,求证在(0,1)内至少存一点 ![]() ,使得
,使得 ![]()