高等数学上学期模拟试题（五）

一、填空题（每小题3分，总15分）

1.设函数 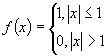，则 .

2. .

3.设 ，则 .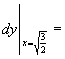

4. .

5.曲线 的弧长等于 .

二、选择题（每小题4分，总20分）

1.设 ，则当 时，（ ）

A. 与 等价无穷小量； B. 与 是同阶但非等价无穷小量；

C. 是比 高阶的无穷小量； D. 是比 低阶的无穷小量。

2.设函数 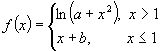，在 处可导，则常数（ ）

A. B.

C. D.

3.设 在 上严格单调减少， 在 处有极大值，则（ ）.

A. 在 处有极小值； B. 在 处有极大值；

C. 在 处有最小值； D. 在 处既无极值也无最小值.

4.若连续曲线 与 在 上关于 轴对称，则积分 的值为（ ）

A. B. C. D.0

5.已知 是可导的偶函数，且 ，则曲线 在（-1，2）处的切线方程是

A. B. C. D.

三、（每小题5分，总15分）

1.设 ，其中 具有二阶导数，且 的一阶导数不等于-1，求

2.求

3.证明：当 时， .

四、（每小题6分，总18分）

1. ，且 ，证明 .

2.已知函数 ，试求：（1） 的单调区间；

（2） 的凹凸区间及拐点；（3）曲线 的渐近线.

3.已知 ，且满足 ，求 .

五、（8分）设函数 在 的某邻域内有4阶连续导数。若 ，而 .试问 是否为极值点：是否为拐点？证明你的结论。

六、（8分）证明方程 在区间（0，1）内有且仅有一个实根。

七、（8分）已知曲线 与曲线 在点 有公共切线，求

（1）常数 的值及切点（ ）；

（2）两曲线与 轴围成的平面图形绕 轴旋转所得旋转体的体积.

八、（8分）设 在闭区间 上有二阶导数，且 ， ，求证：

（1）至少存在一点 使 ；

（2）至少存在一点 ，使 .