高等数学下学期模拟试题（五）
一、填空（每小题3分，共15分，将答案填在题中横线上，不填解题过程）
1.
过两点 
和 
且与平面 
垂直的平面方程是
2.
交换积分次序得 .
3.
曲线 
在点（2，4，5）处的切线与横轴的正向所成的角度是
.
4.
矢量 
在矢量 
上的投影是 .
5.
通解为 
（ 
）为任意常数）的二阶常系数线性齐次微分方程为
.
二、选择题（每小题3分，共15分。每小题有四种选择，有且仅有一个是正确的，将你认为正确的代号填入括号内）
1. 设 
在 
处的全增量为 
，若 在 处可微，则在 处（ ）。
（A） 
； （B） 
；
（C） 
； （D） 
（ 
为高阶无穷小）。
2.
方程 
的特解形式为
( )
（A） 
; （B） 
；
（C） 
; （D） 
。
3. 设 
，则常数项级数 
（ ）。
（A）一定收敛且和为0； （B）一定收敛但和不一定为0；
（C）一定发散； （D）可能收敛，也可能发散。
4. 
为包含原点的任意光滑简单闭曲线，则 
（ ）。
（A）因为 
，所以 
；
（B） 
；
（C）因为 
， 
在 
内不连续，所以 
不存在；
（D）因 
，所以沿不同的 ， 值不同
5. 若 
的三个偏导数存在，且不全为0，则方向 
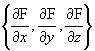是函数 
在点 
处的（ ）。
（A）变化率最大的方向；
（B）变化率最小的方向；
（C）可能是变化率最大的方向，也可能是变化率最小的方向；
（D）既不一定是变化率最大的方向，也不一定是最小的方向。
三、求解以下各题（每小题5分，共25分）
1.
通过点A（-2，3，0）作直线l1，使l1平行于平面 
且和直线 
相交，求直线l1的方程
2.
设 
，求 
.
3.
求 
,其中D为由 
.
4.
设函数 
满足等式 
＝2
＋ ，求 ..
5.
计算 
,其中W是曲面 
, 
所围成..
四、（8分）求级数 
的收敛域，并求和函数
五、（8分）已知函数 
，并给定点 
，求 在 
沿平行于直线 
，且与z轴正向成锐角的方向的方向导数.
六、（8分）.计算 
,其中L为过三点(0,0)、(0,1)、(1,2)的圆周上,顺时针方向从点(0,0)到点(1,2)的一段弧。
七、（8分）计算 
,其中函数f、g、h具有连续导数，∑为平行六面体 
, 
, 
的表面外侧
八、（8分）. 在旋转椭球面 
上求距平面 
最近和最远的点.
九、（5分）证明：若 
=1， 
，则
收敛.