13、设![]() 在
在![]() 内有
内有![]() ,且
,且![]() ,证明在
,证明在![]() 内有
内有![]() .
.
14、试问:方程![]() 总共有几个实根.
总共有几个实根.
15、![]() ,则
,则![]() 。
。
16、设函数![]() 是由
是由![]() (
(![]() )确定,则
)确定,则![]() 。
。
17、设![]() 在区间
在区间![]() 连续,
连续,![]() ,
,
试解答下列问题:(1)用![]() 表示
表示![]() ;(2)求
;(2)求![]() ;(3)求证:
;(3)求证:![]() ;
;
(4) 设![]() 在
在![]() 内的最大值和最小值分别是
内的最大值和最小值分别是![]() ,求证:
,求证:![]() .
.
18、设![]() 为
为![]() 在
在![]() 上应用拉格朗日中值定理的“中值”,则
上应用拉格朗日中值定理的“中值”,则
![]()
19、设![]() ,求
,求![]() 。
。
20、已知函数![]() 在
在![]() 上三阶可导,且
上三阶可导,且![]() ,
,![]() ,
,![]() ,试证至少存在一点
,试证至少存在一点![]() ,使
,使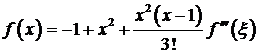 ,
,![]()
21、已知![]() 在
在![]() 上二次连续可微,
上二次连续可微,![]() ,证明
,证明![]()
其中 ![]()
![]() .
.
22、求证方程![]() 有且只有一个实数根,其中常数
有且只有一个实数根,其中常数![]() 满足
满足![]() .
.
23、设![]() 为实数,
为实数,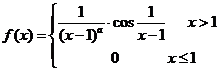 ,在
,在![]() 处可导,求
处可导,求![]() 的范围
的范围
24、设![]() ,
,![]() 是正整数,求
是正整数,求![]()
25、设![]() ,求
,求![]()
26、求方程![]() 有几个实根。 27、设
有几个实根。 27、设![]() ,求
,求![]()
27 设![]() 具有二阶连续导数,且
具有二阶连续导数,且![]() ,
,![]() 是曲线
是曲线![]() 上点
上点![]() 处的切线在
处的切线在![]() 轴的截距,求
轴的截距,求![]() .
.