四、级数
1、判别级数的敛散性
(1)![]() ;
(2)
;
(2) 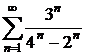
(3)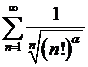 ,其中
,其中![]() 为常数 (4)
为常数 (4)![]()
2、求和函数
(1)![]() (2)
(2)![]() (3)
(3)![]()
(4)![]() (5)
(5)![]()
3、求收敛域
(1)![]() (2)
(2)![]()
4、已知级数![]() 的一般项
的一般项![]() 与前
与前![]() 项的和
项的和![]() 有如下关系:
有如下关系:
![]() (
(![]() ),且
),且![]() ,求级数
,求级数![]()
5、设![]() (
(![]() ),则
),则![]() 。
。
6、设![]() ,
,![]() ,证明级数
,证明级数![]() 收敛,并求其和。
收敛,并求其和。
7、设![]() 在
在![]() 处收敛,则
处收敛,则![]() 在
在![]() 处( D )
处( D )
(A) 绝对收敛; (B) 条件收敛; (C) 发散; (D) 收敛性与an有关.
8、设幂级数 ![]() , 当
, 当![]() 时
时![]() ,且
,且![]() ;
;
(1)求幂级数![]() 的和函数
的和函数![]() ;(2)求和函数
;(2)求和函数![]() 的极值..
的极值..
9、求函数![]() 的定义域,并证明
的定义域,并证明![]() 在定义域内有界.
在定义域内有界.
10、级数![]() ,问
,问![]() 为何值时级数收敛
为何值时级数收敛